We always look forward to the final round of group games, and they delivered some serious drama. In particular, Germany's desperate search for a goal against South Korea will live long in the memory, as will Iran's late surge to give the Portuguese a huge scare.
Out of the 16 teams to qualify for the finals, Portugal, Argentina and Japan were one goal away from being eliminated, whilst Spain and Mexico were a goal away from elimination until added time in their matches. Argentina take the crown of the team who sneaked into the qualification spots the latest, thanks to Marcos Rojo's improbable late goal.
Second round
For the second round, calculating each team's probabilities of progression is easy - now the matches are drawn we can just take the odds directly. As before, we take the probability of a draw and split it evenly between the team sides. This leads to the following probabilities for the next round:
| Uruguay 51% - 49% Portugal France 56% - 44% Argentina Brazil 74% - 26% Mexico Belgium 78% - 22% Japan | Spain 73% - 27% Russia Croatia 66% - 34% Denmark Sweden 48% - 52% Switzerland Colombia 40% - 60% England |
Now, things become more complicated. Our old method involved taking each team's odds of winning the whole tournament and transforming them into odds. However, this will now be highly conditional on each team's route to the trophy, particularly given the unbalanced nature of the draw.
Therefore, we have used a statistical concept called conditional probability to estimate each team's success. If you want to read the explanation, click below. If not, just skip to the next section.
This, however, is highly dependent on their second-round match. For example, Mexico have a meagre 9% chance of winning their quarter-final, but a large part of that will be due to the fact they have Brazil in the second round, and are therefore unlikely to even be in the quarter-finals.
To correct for this, we simply divide each team's chances of winning the later round by their chances of winning the previous round. So, for Mexico to win in the quarters, we would divide 9% by 26% to give 35.9%.
Of course, it's unlikely that the other team in the semi-final will have exactly 64.1% chance of winning. So we smooth out the two teams' probabilities by dividing each one's by the total between the two teams.
So, say Mexico (35.9% chance of winning their quarter) face Belgium. The Belgians are rated as 47.4% likely to win their quarter. We then add 35.9% and 47.4% to get 83.3%, and divide each team's chance by this sum - giving a final probability of 43.1% for Mexico and 56.9% for Belgium.
We can repeat this method for the semi-finals (by starting with each team's 'chance of reaching the final' divided by their 'chance of reaching the semi-final'), and again for the final itself.
So, let's run our model our standard 3,000 times to see how each team does!
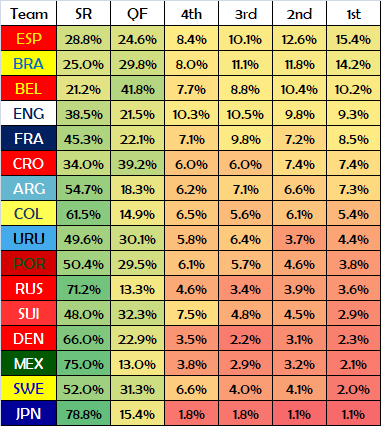
We previously had a 'big eight' (Brazil, Germany, Spain, France, Argentina, Belgium, England and Portugal). Now it is probably fair to say that there is a 'big seven', with Croatia replacing Germany and Portugal dropping out.
Tantalisingly, the tournament looks wide open. But anyway, let's answer the question everybody has been asking:
Were England right to finish second?
Before I start answering that, I do take exception to the question. Watching the game last night I thought England didn't deliberately try to finish second, nor did Belgium. I would agree that England didn't bust a gut to level, but I don't see why they should - regardless of the complicated situation regarding the draw.
Had Japan beaten Poland to win Group H, this would have been a much simpler question - the answer would have been a definite yes.
As it is, Belgium face the easier second round match, with only a 21.2% chance of going out at this stage, compared to England's 38.5%.
It's the quarter-finals though where everybody had been focusing. We can see that Belgium only have a 37.0% chance of reaching the semis, compared to England's 40.0% - thanks to the Brazil effect.
The semi-finals are quite interesting. England are most likely to face Spain or Croatia, whilst Belgium could realistically meet any of Uruguay, Portugal, France or Argentina. Neither prospect is particularly generous, and so from here we would expect matters to be equal. As it is, Belgium have a higher chance of reaching the final (20.6%) compared to England (19.1%).
In summary, it appears to be much of a muchness, finishing first or second in Group G. And because there's little apparent difference in outcome, I think Gareth Southgate was justified in resting key players and making sure everybody has had World Cup experience.
Summary
As always, our World Cup page has been updated with the latest version of the model. We are now getting a very clear idea of each team's chances.
I am pretty hopeful of there being a new name in this year's World Cup final. In particular, the lower half of the draw only features Spain as a regular tournament finalist, and they only have a 28.0% chance of making the showpiece this year - so will we see a new name on the trophy this year?

 RSS Feed
RSS Feed