Introduction
Last week we unveiled the TGIAF simulator for the 2014 World Cup. Now, we are going to run our simulator a thousand times, and look at our eventual output.
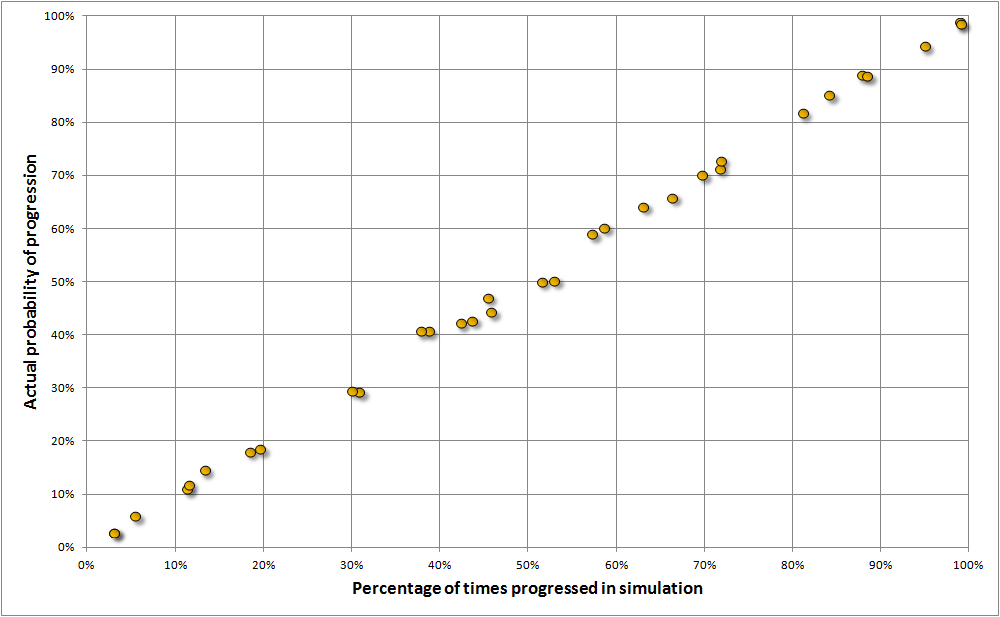
Firstly, we need to know if a thousand simulations is a big enough sample size to accurately replicate the true probability of an event happening.
Testing our Simulations
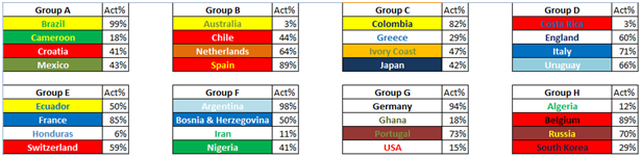
We have worked out the true probabilities that each side qualifies from its group. The method used to find these probabilities is fairly arduous, for details see Appendix 1. For these to be ‘true’ probabilities, we are assuming that the bookies’ odds for each individual match is a representation of the true likelihood of each possible result in each match. For justification of this, see our earlier article on interpreting odds.
If we plot the probabilities that each team qualify from their group against the percentage of times they qualify from their group in our simulations, we get the following graph:
Simulation Results
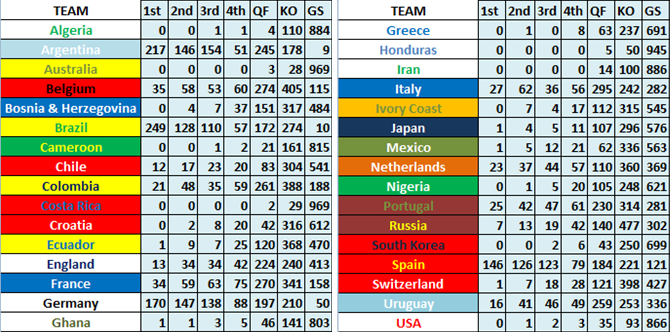
For each simulation, we have taken note of where each team finishes, and counted how many times they finished in each stage. The results of this can be seen below:
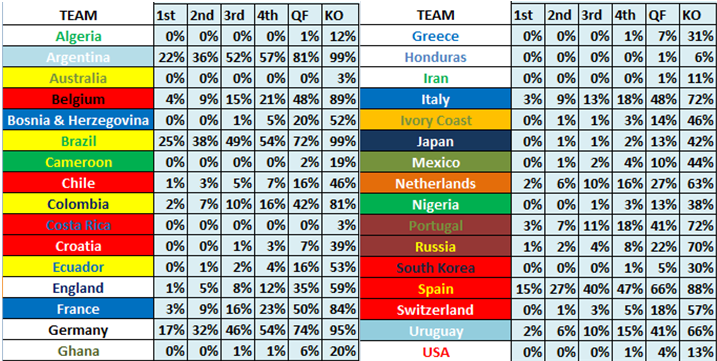
We can convert these values into cumulative probabilities showing the chances of reaching each stage:
Needless to say, where our table says “0%”, it does not mean there is zero chance of that likelihood happening, it is just rounded down, so it means there is a less than 0.5% chance of that event occurring.
So Who Will Win?
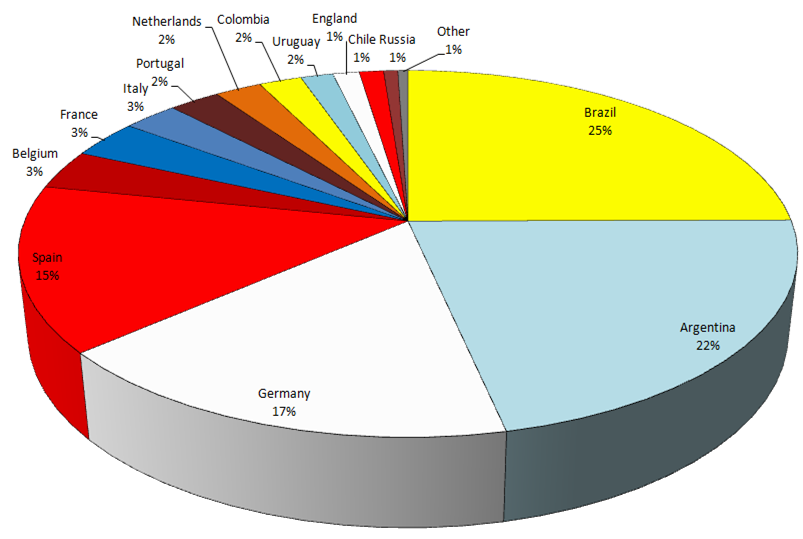
The graph below shows the proportion of the time each team won the World Cup in our simulation. This can be taken as the probability that they will indeed go on to win in Brazil this year.
The next category is the chasing pack, teams who are unlikely to win the tournament, but who could see a challenge materialise with the right results.
And the final category is the big four: Brazil, Argentina, Germany and Spain, who are the realistic contenders to lift the Jules Rimet trophy, and for whom anything less than a semi-final spot will be seen as a failure and a missed opportunity.
Conclusion
As mentioned when we unveiled our simulator, a one-off simulation does not tell us anything worthwhile about what might happen in this summer’s tournament. However, by running the simulator multiple times, the overall patterns can be seen.
We will be able to use these powerful results in order to see if there are any longer-term odds which are under- or over-priced.
In a given World Cup group, there are 6 matches, each with 3 possible outcomes. Therefore the number of possible combinations of results is 3^6 = 729.
For each of these combinations, the probability of it occurring needs to be calculated. This is achieved by multiplying the probability of all six results together, which can be expressed as:
p[c] = p[1] x p[2] x p[3] x p[4] x p[5] x p[6]
Where p refers to a probability, c is the combination, and 1, 2, etc are the six matches.
We then need to work out which teams qualify, given a particular combination of matches. Firstly, the points total for each team is found. If two teams are distinctly clear in the top two positions, then clearly they are the ones to progress, and are given the value 1 (the probability they go through), whilst the other teams are given a value of 0.
However, there are a number of scenarios where multiple teams can finish level on points across the boundary for qualification. The simplest of these is when two teams are level on points, and take up 2nd and 3rd position. In this case, the two teams are given a value of 0.5. The same applies when all four are level on points.
The next scenario is when three teams are tied in 1st, 2nd and 3rd place. In this case, each team is given the value 2/3, since that is the chance they progress from this stalemate (as we do not take goal difference into account). Similarly, for three teams tied in 2nd, 3rd and 4th position, they are given values of 1/3 each.
If we now multiply the chance of progression for each team by the chance of each possibility occurring, and sum all 729 resulting values for each side, we get their overall probability of progressing from the group. Below is the list of each team’s probability of getting to the group stages:

 RSS Feed
RSS Feed